Technip Energies Online Exclusive: The benefits of homomorphic encryption: A technological enabler for digital services to operations
Fabrice Rey and Mathieu Sanchez, Technip Energies; and Aymen Boudguiga, Université Paris-Saclay, CEA-List
Among the cryptographic technologies under development in various industries, homomorphic encryption possesses the attractive feature of allowing computation within the encrypted domain. Encrypted data cannot only be transferred and stored, but also used in the secure encrypted state. This state-of-the-art technology evolved rapidly over the past decade with new breakthroughs every year since the first functional implementation in 2009. The technology already is proposed for face recognition and in other domains where a high level of privacy is mandatory.
This article presents the main principles of homomorphic encryption. It explores benefits that can be leveraged from this technology for the energy industry. It also provides information on the specific challenges faced in its implementation within industry.
With the advent of Industry 4.0, the digital transformation of a company embeds the exploitation of all available plant data to enhance monitoring, planning and optimization of the operating parameters. This is designed to maximize the production rate at minimal cost. As an example, predictive maintenance solutions analyze performance and operating data from rotating equipment to detect any potential failure as early as possible using tools that combine machine learning and artificial intelligence methods.
Often overlooked or underused, plant operating data constitutes an important and full-fledged asset of the company that should be properly valued and secured internally or by third-party expertise.
In the cases where data cannot be used internally and must be transmitted to an external service provider, the data owner can be reluctant to share such confidential information in plain text with a third party for various reasons. This data includes protected intellectual property on the company's facilities, financial statements and results, and sensitive information with national security implications.
How can it be guaranteed that a company’s confidential data can be outsourced safely by certifying that the content will not be readable by a third party in charge of its processing?
There are many competing technologies for data encryption. Among the main technologies, symmetric cryptography such as advanced encryption standard (AES) and asymmetric cryptography such as Rivest-Shamir-Adleman (RSA) or El Gamal are widely used when navigating on the web and/or for online payment. These cryptography algorithms are recognized for their fast computation time while providing an important level of security for data at transit and data at rest. However, data must be deciphered for any use in computation. As such, these algorithms are not fit for the use of confidential data by a third party.
Therefore, other algorithms are proposed for more advanced applications. For example, multiparty computation (MPC) is adopted in digital asset protection and cryptocurrency. Though MPC enables the performance of mathematical operations on encrypted data, the result of the computation can be available to all parties. One of the specifics of the MPC scheme is it also requires an elevated level of cooperation between parties as the computation algorithm must be shared.
When compared to these technologies (e.g., classical cryptographic algorithms AES or RSA), homomorphic encryption adds computation confidentiality to data confidentiality at transit and at rest ensured by AES or RSA. It also alleviates the communication overheads introduced when using MPC.
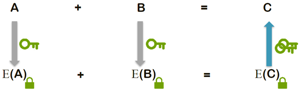
Enabling safe and secure computations. Homomorphic encryption is a form of encryption that allows computation on encrypted data, generating an encrypted result which, when decrypted, matches the result of the operations as if it had been performed on plain text. This means encrypted data can be securely and safely outsourced for computation by third parties.
In a case example, “Alice” will encrypt and transmit her sensitive data to “Bob” who oversees data analysis and computation. The homomorphic property of the encryption algorithm allows Bob to perform these calculations directly on the encrypted data and obtain an encrypted result. The latter is an encrypted version of the result that would be recovered if Bob’s computation were done directly on Alice’s plain texts.
As shown in FIG. 1, Alice receives the encrypted results of the operation from Bob. Alice uses the decryption key to recover the results and then exploit them. Only Alice, owner of the private key used for decryption, will be able to read and understand the results of the calculation performed by Bob.
Bob, in charge of the data computation, will never have access to the data in plain text, neither input nor calculation results. On the other side, the details of calculation algorithms remain Bob’s intellectual property and are not disclosed to Alice.
Homomorphic encryption can be symmetric or asymmetric. In the first case, the encryption and decryption key will be the same “secret key.” Meanwhile, in the second case, the encryption and decryption keys will be different but related. The encryption key is also called the “public key” and is shared with any party. The decryption key must remain private and serves only for data decryption. The owner of the private key is the only entity capable of decrypting the data encrypted with its corresponding public key.
Homomorphic encryption: Introduced in 1978. The homomorphic encryption idea was introduced in 1978 by Rivest et al., but no true fully homomorphic encryption (FHE) scheme was developed for years. However, research and improvement has accelerated in the last decade. In 2009, Gentry made a breakthrough by specifying the first FHE scheme allowing summing and multiplying ciphertexts. Many encryption schemes then were specified and regularly optimized with the recognized 4th generation of the FHE schemes [Cheon-Kim-Kim-Song (CKKS) scheme in 2016]. With these improvements, it has been calculated that homomorphic encryption execution was getting eight times faster every year between 2011–2021, as explained by Gentry at Eurocrypt conference in 2021. This fast-tracks improvement of the technology has made it applicable to daily life in recent years.
As examples of already implemented homomorphic encryption, the following are the most noteworthy:
- Critical infrastructure monitoring such as electrical network load and balance
- Health data, including sharing private medical records for statistical studies
- Pay-as you-drive insurance, with an attached analytical device that gauges driving style
- Passport face recognition at the airport.
The current state-of-the-art, homomorphic encryption supports the basic mathematical operations of summation and multiplication. This opens to a wide variety of applications, as these two operations are sufficient to define a large spectrum of algebra.
However, homomorphic encryption requires a lot of computational resources to perform operations within the encrypted space. Computation time of a single simple equation may take up to a few seconds to perform. That is the cost for the high privacy proposed by homomorphic encryption.
Due to these limitations, the use of homomorphic encryption must be carefully investigated to ensure selecting the most adequate homomorphic encryption algorithm for a given application. In the energy industry, this technology is of particular interest in the use of production data. These production data are usually considered extremely sensitive information, as their disclosure may impact companies’ share or product prices. This sensitivity of production data is a showstopper for the implementation of digital services to operations as all inputs to these services must remain within the company’s operating information management ecosystem. Therefore, subcontracting specialized computation to vendors or contractors is not considered an option by operating companies.
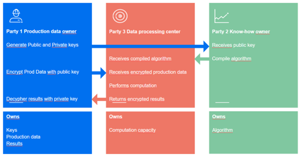
A three-party scheme. Using homomorphic encryption, it becomes possible to have a scheme that includes up to three different parties in a straightforward way. The first party is the industrial site, the owner of the production data. This first party is interested in using external expertise resources but does not wish to disclose the production data. The second party is a vendor or contractor that has developed internal expertise and is willing to provide results in a near real-time manner to the first party. However, the second party wishes to retain its intellectual property on the knowledge. Lastly, the third party possesses huge processing capabilities and is willing to host the near real-time service. This overall scheme is outlined in FIG. 2.
FIG. 2 illustrates how energy industry benefits can be leveraged from the homomorphic encryption to run near real-time online processes and operations analysis without disclosing production data.
The protocol can be declined in several two-party schemes, considering that two of the three mentioned parties are the same. Each of these two-party schemes would serve different purposes, such as confidentiality during cloud computing or confidentiality of algorithms and data.
The capacity to treat production data in near real time while maintaining the privacy of the production data is appealing to the energy industry. It is an enabler for the development of digital services based on data reconciliation and analysis. However, even if the technology is answering some of the key questions for this kind of service, it still must prove effective in the context of the energy industry.
Cooperation yields interesting results. The authors’ companies partnered in a development project to evaluate the application of homomorphic encryption to a realistic problem in the energy industry. A case study was selected regarding the monitoring and production tracking of a debutanizer column. A process dynamic simulation model was developed as the asset providing the data from the industrial site. In addition, some computation to be applied through the homomorphically encrypted program were defined.
At the early stage of the project, two key issues were soon highlighted. The first issue is that results from the homomorphic calculations must be contextualized in time for a good understanding of the results. The second issue dealt with the kind of data that is generated within the industry.
For contextualization, the issue was easily overcome by adding a time stamp on the data. Therefore, even during a steady operation of the plant that would generate two identical sets of process conditions otherwise, the external observer would not witness status quo information.
In the energy industry, engineers and operators are used to working with a broad range of real values to characterize plant behavior. The common feature for all the already developed applications is that the encrypted input data are minimal in terms of digital space. They are mostly coded over short integer data when they are not binary. With homomorphic encryption, the computation time will be related to the number of bits required to represent the information. Initial assessment resulted in several minutes for a sum product calculation when encrypting bits separately using a binary plain text space. Further development with encryption schemes supporting modular arithmetic with large plain texts brought a sharp decrease in calculation time from several minutes to a few seconds without loss of significance.
One of the functions evaluated during the research was an economic evaluation of the debutanizer’s performance. This evaluation is made from “customer” encrypted production data and from clear parameters on product prices that can be set from market prices.
The encrypted inputs were the following:
- Feed mass flow—F1
- Fuel gas mass flow—F2
- Liquefied petroleum gas mass flow—F3
- Stabilized naphtha mass flow—F4
- Hot oil mass flow—F5
- Hot oil inlet temperature—T1
- Hot oil outlet temperature—T2.
The market prices inputs were the following:
- Unstable naphtha price/t—K1
- Fuel gas price/t—K2
- Liquefied petroleum gas price/t—K3
- Stabilized naphtha price/t—K4
- Hot oil properties—K5.
The output O1 (in USD) is expressed as:
O1 computation time with the Brakerski-Fan-Vercauteren (BFV) encryption scheme from Microsoft SEAL library was 0.033 seconds when encrypting large plain texts (around 32 bits long). Note: Two pre-analyses were conducted to fix the size of plain texts and choose the suited homomorphic encryption algorithm for O1 computation (i.e., to choose the BFV encryption scheme from Microsoft SEAL library). First, O1 was computed over clear real numbers to obtain the expected output values and their ranges. Then, the authors computed it over clear integers obtained by rescaling the clear real inputs. Computing O1 with rescaled integers introduced a loss of precision. The authors fixed the rescaled integers size to ensure a two-digits precision in the significand. This worked with clear integers longer than 32 bits. Then, as O1 computation consists only in addition and multiplication of integers, the authors chose to use a homomorphic encryption scheme supporting modular arithmetic with large inputs such as BFV in Microsoft SEAL library or Brakerski, Gentry and Vaikuntanathan (BGV) in IBM Helib. The authors did not choose to use libraries working with binary plain texts, by encrypting separately the bits of inputs (such as the TFHE library), as O1 computation in that case would take around 1 min.
However, with the Microsoft SEAL implementation of the BFV scheme used to reach this performance, it was not possible to perform a comparison on real numbers that also were part of the evaluation. Therefore, the final demonstrator integrated two different implementations relying on two different homomorphic encryption schemes, one with the TFHE scheme and a binary plain text space and the other with the BFV scheme and covering large numbers to minimize computation time. The functions evaluated with TFHE enclosed an encrypted comparison. The functions computed with BFV required only additions and multiplications. The outcome of the work performed on the demonstration test case was that the 20 tested functions were evaluated every 10 sec without lag with a standard 4 core server.
The research work performed on applicability of homomorphic encryption schemes in the energy industry proved successful thanks to the cooperation between the authors companies. At the start of the project, the forecast of computation time was not satisfying and seemed to be a showstopper in the current state of the research. However, creative solutions were found to overcome this initial assessment and ended in a workable demonstrator hosted in a standard virtual machine.
Online digital services in the energy industry can be made easier from a contractual standpoint with the use of homomorphic encryption. It secures actors in their respective confidential production data and intellectual properties for this kind of project.
Homomorphic encryption extends a plant optimization program performed on selected historical data to a near real-time application. Algorithms crafted from historical data in the traditional ways can be converted into an online homomorphically encrypted application that keeps providing operations information and advice.
REFERENCES
1 Rivest, R., L. Adleman and M. Dertouzos, “On data banks and privacy homomorphisms,” Massachusetts Institute of Technology, Cambridge, Massachusetts, 1978, online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.500.3989&rep=rep1&type=pdf
2 Gentry, C., “Fully homomorphic encryption using ideal lattices,” Symposium on Theory of Computing (STOC), 2009.
3 Cheon, J. H., A. Kim, M. Kim and Y. Song, “Homomorphic encryption for arithmetic of approximate numbers,” ASIACRYPT, 2017.
4 Boura, C., N. Gama, M. Georgieva and D. Jetchev, “CHIMERA: Combining ring-LWE-based fully homomorphic encryption schemes,” Journal of Mathematical Cryptology, 2019.
5 Gentry, C., “A decade (or so) of fully homomorphic encryption,” Eurocrypt, 2021, online: https://eurocrypt.iacr.org/2021/slides/gentry.pdf






Comments